What Is Half Of 3/4
regarder
Sep 24, 2025 · 5 min read
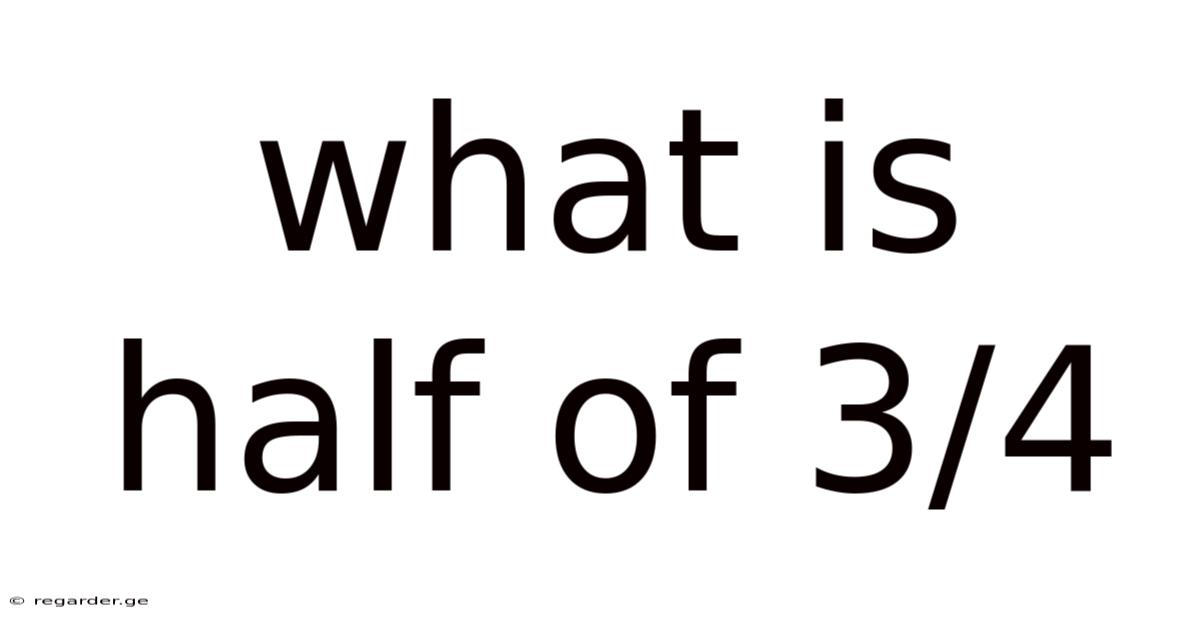
Table of Contents
What is Half of 3/4? A Deep Dive into Fractions and Their Applications
Finding half of 3/4 might seem like a simple arithmetic problem, suitable only for elementary school. However, understanding this seemingly basic calculation unlocks a deeper appreciation for fractions, their manipulation, and their widespread applications in various fields. This article will not only answer the question "What is half of 3/4?" but will also explore the underlying mathematical concepts, practical applications, and address common misconceptions. We'll delve into the world of fractions, empowering you to confidently tackle similar problems and understand the logic behind fractional calculations.
Understanding Fractions: A Foundational Review
Before we tackle the core question, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we have 3 parts out of a possible 4 equal parts.
Key Concepts:
- Numerator: The top number, representing the number of parts.
- Denominator: The bottom number, representing the total number of equal parts.
- Proper Fraction: A fraction where the numerator is smaller than the denominator (e.g., 3/4).
- Improper Fraction: A fraction where the numerator is greater than or equal to the denominator (e.g., 5/4).
- Mixed Number: A number containing both a whole number and a fraction (e.g., 1 1/4).
Calculating Half of 3/4: The Step-by-Step Process
Now, let's address the central question: What is half of 3/4? There are several ways to approach this problem, each illustrating different aspects of fractional arithmetic.
Method 1: Direct Multiplication
The most straightforward approach is to multiply 3/4 by 1/2. Remember that "of" in mathematics often implies multiplication.
- Step 1: Write the expression: (1/2) * (3/4)
- Step 2: Multiply the numerators together: 1 * 3 = 3
- Step 3: Multiply the denominators together: 2 * 4 = 8
- Step 4: Combine the results to form the new fraction: 3/8
Therefore, half of 3/4 is 3/8.
Method 2: Dividing by 2
Alternatively, we can interpret "half of 3/4" as dividing 3/4 by 2. Dividing by 2 is the same as multiplying by 1/2.
- Step 1: Write the expression: (3/4) / 2
- Step 2: Rewrite the division as multiplication by the reciprocal of 2 (which is 1/2): (3/4) * (1/2)
- Step 3: Proceed as in Method 1, resulting in 3/8.
This method reinforces the connection between division and multiplication with fractions.
Method 3: Visual Representation
A visual approach can enhance understanding. Imagine a square divided into four equal parts. Shade three of these parts to represent 3/4. Now, divide the shaded area in half. You'll find that you've shaded 3 out of 8 equal parts of the original square, confirming that half of 3/4 is 3/8. This visual method makes the concept more intuitive, particularly for beginners.
Expanding the Understanding: Applications of Fractions
The seemingly simple calculation of half of 3/4 has far-reaching implications and applications across various fields:
-
Cooking and Baking: Recipes often involve fractional measurements. Understanding fractions is crucial for accurately scaling recipes up or down. For example, if a recipe calls for 3/4 cup of flour, and you want to halve the recipe, you'll need 3/8 cup of flour.
-
Construction and Engineering: Precision is paramount in these fields. Fractions are used extensively in measurements, calculations, and blueprints. Understanding fractional relationships is essential for creating accurate and stable structures.
-
Finance and Accounting: Fractions are used to represent portions of ownership, interest rates, and other financial calculations. Understanding fractional arithmetic is crucial for accurate financial modeling and analysis.
-
Data Analysis and Statistics: Fractions often appear in representing proportions and probabilities. Accurate fractional calculations are vital for interpreting data and drawing meaningful conclusions.
-
Computer Science: Fractions are used in algorithms, data structures, and image processing. Efficient and accurate fractional arithmetic is vital for the proper functioning of many computer programs.
Addressing Common Misconceptions
Several common misconceptions surround fractional calculations. Let's clarify some of them:
-
Adding Numerators and Denominators: A frequent mistake is adding the numerators and denominators directly. For example, incorrectly assuming that 1/2 + 1/4 = 2/6. Remember, you must find a common denominator before adding or subtracting fractions.
-
Multiplying Numerators and Denominators Only in Addition/Subtraction: It's crucial to remember that only multiplication and division allow for direct multiplication of numerators and denominators. Addition and subtraction require a common denominator.
-
Incorrect Reciprocal: When dividing fractions, remembering to take the reciprocal of the second fraction (flipping it) is crucial. Incorrectly applying the reciprocal can lead to erroneous results.
-
Misinterpreting Mixed Numbers: Converting between mixed numbers and improper fractions needs careful attention. Understanding this conversion is crucial for simplifying calculations involving mixed numbers.
Frequently Asked Questions (FAQ)
Q: Can I simplify 3/8 further?
A: No, 3/8 is already in its simplest form. The numerator (3) and denominator (8) have no common factors other than 1.
Q: How do I convert 3/8 to a decimal?
A: To convert 3/8 to a decimal, divide the numerator (3) by the denominator (8): 3 ÷ 8 = 0.375
Q: How would I calculate double of 3/4?
A: To calculate double of 3/4, you would multiply 3/4 by 2, which is equivalent to (3/4) * (2/1) = 6/4. This simplifies to 3/2 or 1 1/2.
Conclusion: Mastering Fractions – A Lifelong Skill
Understanding fractions is a fundamental skill applicable across many aspects of life. While finding half of 3/4 might appear trivial at first glance, the process reveals the underlying principles of fractional arithmetic and their significance in various fields. By mastering these concepts, you enhance your problem-solving abilities and open doors to a deeper understanding of mathematics and its practical applications. Continue practicing, exploring different approaches, and don't hesitate to visualize these concepts to build a strong foundation in fractional arithmetic. The ability to confidently handle fractions is a valuable asset, applicable far beyond the classroom. Remember that consistent practice and a clear understanding of the underlying principles are key to mastering this crucial mathematical skill.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is Half Of 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.