3 Out Of 8 Percentage
regarder
Sep 24, 2025 · 5 min read
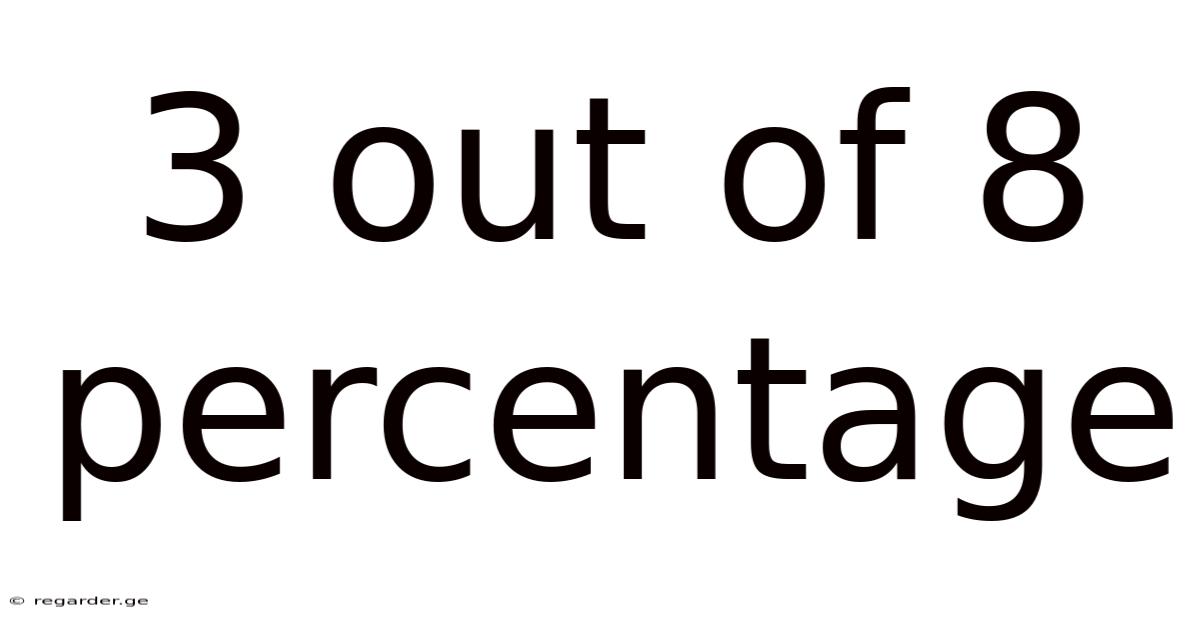
Table of Contents
Understanding 3 Out of 8: Percentage, Fraction, and Real-World Applications
Understanding fractions and percentages is a fundamental skill in mathematics with broad applications in everyday life. This article delves into the meaning of "3 out of 8," exploring its representation as a fraction, a decimal, and a percentage, along with numerous real-world examples to solidify your understanding. We'll also cover some common misconceptions and explore how to confidently tackle similar problems. This comprehensive guide will equip you with the tools to effortlessly navigate percentage calculations and their practical implications.
What Does "3 Out of 8" Mean?
The phrase "3 out of 8" signifies a proportion or ratio. It indicates that 3 items represent a specific portion of a total of 8 items. This simple statement can be expressed in several ways, each with its own advantages depending on the context.
Representing "3 Out of 8" as a Fraction
The most direct representation of "3 out of 8" is as a fraction: 3/8. The numerator (3) represents the number of items we're interested in, while the denominator (8) represents the total number of items. This fraction is in its simplest form because 3 and 8 share no common factors other than 1.
Converting the Fraction to a Decimal
To convert the fraction 3/8 into a decimal, we simply divide the numerator (3) by the denominator (8):
3 ÷ 8 = 0.375
Therefore, "3 out of 8" is equivalent to 0.375 as a decimal.
Calculating the Percentage
To express "3 out of 8" as a percentage, we first convert the fraction to a decimal (as shown above: 0.375). Then, we multiply the decimal by 100 and add the "%" symbol:
0.375 × 100 = 37.5%
So, "3 out of 8" represents 37.5%. This means that 3 items constitute 37.5% of the total 8 items.
Real-World Applications of "3 Out of 8" and Percentage Calculations
The concept of "3 out of 8" and its equivalent percentage (37.5%) has numerous applications in various aspects of daily life. Let's explore some examples:
-
Test Scores: Imagine you answered 3 questions correctly out of a total of 8 questions on a quiz. Your score would be 37.5%. This allows you to quickly understand your performance relative to the total possible points.
-
Surveys and Polls: If 3 out of 8 people surveyed preferred a particular product, the preference rate for that product would be 37.5%. This data is crucial for market research and product development.
-
Sports Statistics: In baseball, if a batter gets 3 hits out of 8 at-bats, their batting average is 37.5%. This is a vital statistic that helps assess a player's performance.
-
Financial Calculations: Suppose you invested in a portfolio where 3 out of 8 investments experienced growth. This represents a 37.5% growth rate among your investments. This helps in evaluating the success rate of your investment strategies.
-
Manufacturing and Quality Control: If 3 out of 8 manufactured items are found to be defective, the defect rate is 37.5%. This information is critical for improving production processes and ensuring quality.
-
Probability: In probability theory, if there are 8 equally likely outcomes and 3 of them are favorable, the probability of a favorable outcome is 3/8 or 37.5%. This is a fundamental concept in determining the likelihood of different events.
Understanding Proportions and Ratios
The concept of "3 out of 8" is intrinsically linked to proportions and ratios. A ratio is a comparison of two quantities, often expressed as a fraction (e.g., 3:8 or 3/8). A proportion is a statement that two ratios are equal. Understanding these concepts allows for the solution of more complex problems involving percentages.
For example, if we know that 3 out of 8 apples are red, and we have a larger batch of 24 apples, we can use proportions to determine how many red apples are in the larger batch:
3/8 = x/24
Solving for x (the number of red apples):
x = (3 × 24) / 8 = 9
Therefore, there are 9 red apples in the larger batch of 24 apples.
Addressing Common Misconceptions
Many people struggle with percentage calculations, often due to misconceptions. Let's address some common errors:
-
Confusing Percentage with Decimal: Remember that a percentage is a fraction out of 100. To convert a decimal to a percentage, multiply by 100. To convert a percentage to a decimal, divide by 100.
-
Incorrectly Calculating Percentages of Percentages: Calculating percentages of percentages requires careful attention to order of operations. For example, a 10% discount followed by a 20% discount is not a 30% discount.
-
Misinterpreting Data: Always carefully consider the context of the data. For example, a 10% increase in sales might sound impressive, but if the initial sales were very low, the actual increase might be insignificant.
-
Overlooking the Whole: Always make sure you are clear about what the "whole" represents. In the "3 out of 8" example, the "whole" is 8.
Frequently Asked Questions (FAQs)
Q: How do I calculate a percentage increase or decrease?
A: To calculate a percentage increase, find the difference between the new value and the original value, divide by the original value, and then multiply by 100. For a percentage decrease, follow the same steps but use the absolute value of the difference.
Q: What if the numbers are not whole numbers?
A: The same principles apply. Convert the numbers to decimals or fractions as needed and perform the calculations accordingly.
Q: How can I improve my understanding of percentages?
A: Practice is key! Work through various examples, starting with simple problems and gradually increasing the complexity. Use online resources and practice exercises to build your skills.
Q: Why are percentages important?
A: Percentages provide a standardized way to compare and interpret data from various sources, making them essential for decision-making across many fields.
Conclusion
Understanding "3 out of 8" and its equivalent percentage, fraction, and decimal representation is a crucial skill with far-reaching implications. From analyzing test scores to interpreting market research data, the ability to accurately calculate and interpret percentages is invaluable in various aspects of life. By mastering these fundamental concepts, you'll be better equipped to navigate numerical challenges confidently and effectively in your personal and professional endeavors. Remember to practice regularly, and don't hesitate to consult resources or seek help when needed. The journey to mathematical proficiency is a rewarding one, and understanding percentages is a vital step along the way.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3 Out Of 8 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.